
8. Centre of mass
The momentum of a closed mechanical system has different values in different (inertial) frames of reference. If a frame K’ moves with velocity V relative to another frame K, then the velocities $$v_{a}^{`} $$ and $$v_{a}$$ of the particles relative to the two frames are such that $$v_{a} = v_{a}^{`} +V$$ The momenta P and P' in the two frames are therefore related by $$\textbf{P} = \sum_a m_a \textbf{v}_a = \sum_a m_a \textbf{v}_a^{`} + \textbf{V} \sum_a m_a $$ or $$\textbf{P}=\textbf{P`} +\textbf{V} \sum_a m_a $$
In particular, there is always a frame of reference K' in which the total momentum is zero. Putting P' = 0 into the previous equation, we find the velocity of this frame: $$ \textbf{V} = \textbf{P}/ \sum_a m_a \textbf{v}_a = \sum_a m_a \textbf{v}_a / \sum_a m_a $$
The right-hand side of the above formula can be written as the total time derivative of the expression $$ \textbf{R} = \sum_a m_a \textbf{r}_a / \sum_a m_a (8.1)$$ We can say that the velocity of the system as a whole is the rate of motion in space of the point whose radius vector is (8.1). This point is called the centre of mass of the system.
9. Angular momentum
Let us presently infer the conservation law which takes after from the isotropy of space. This isotropy implies that the mechanical properties of a closed system do not change when it is rotated as a entire in any way in space.
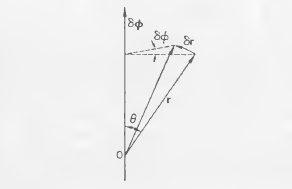
We shall use the vector $$\overrightarrow{\partial \phi} $$ of the infinitesimal rotation, whose magnitude
is the angle of rotation $$\partial \phi $$ and whose direction is that of the axis of rotation.
Let us find, first of all, the resulting increment in the radius vector from
an origin on the axis to any particle in the system undergoing rotation. The
linear displacement of the end of the radius vector is related to the angle by
$$|\partial r| = r sin(\theta) \partial \phi $$(Fig. 1). The direction of $$\partial r$$ is perpendicular to the plane
of r and $$\partial \phi $$ Hence it is clear that
$$\partial r = \overrightarrow{\partial \phi} \times r$$


Problems
Problem 1. Obtain expressions for the Cartesian components and the magnitude of the angular momentum of a particle in cylindrical co-ordinates $$r, \phi, z$$ My Answer: $$ x = r cos\phi, y = r sin\phi, z=z$$ $$ M_x = \sum_a m(y_a \dot{z}_a - z_a \dot{y}_a)$$ $$ M_y = \sum_a m(z_a \dot{x}_a - x_a \dot{z}_a)$$ $$ M_z = \sum_a m(x_a \dot{y}_a - y_a \dot{x}_a)$$ => $$ M_x = m(r sin \phi \dot{z} - \dot{r} sin \phi z - r cos(\phi)\phi z)$$ $$ M_y = m(- z r sin \phi \phi + \dot{r} cos \phi z - r cos(\phi)\phi \dot{z})$$ $$ M_z = m r^{2} \phi $$ $$M^{2} = M^{2}_x+M^{2}_y+M^{2}_z=m^{2}r^{2}\phi^{2}(r^{2}+z^{2}) + m^{2}(r\dot{z}-z\dot{r})^{2}$$ Problem 2. The same as Problem 1, but in spherical co-ordinates $$r, \theta, \phi$$ My Answer: Spherical coordinate system