
11. Line, surface and volume integrals
Problem 11.1 The vector field F is defined by F = $$2xzi + 2yz^{2}j + (x2 + 2y^{2}z − 1)k$$. Calculate ∇ × F and deduce that F can be written F = ∇φ. Determine the form of φ.
My Answer:
$$∇ × F$$ =
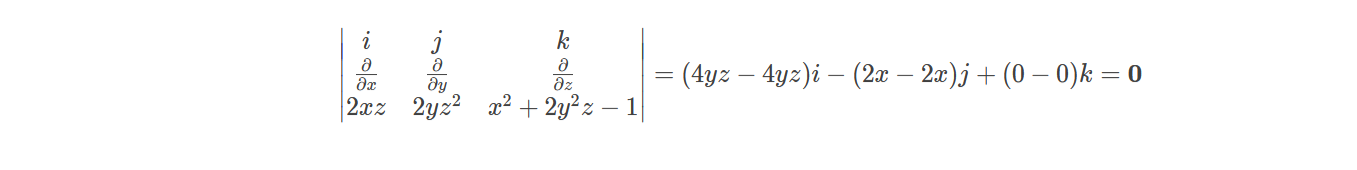
The fact that it is implies that F can be written as ∇φ for some scalar φ. Let $$F=∇φ$$, $$2xz = \frac{\partial φ}{\partial x}$$=>$$x^{2}z + g(y, z) = φ$$ $$2yz^{2} = \frac{\partial g}{\partial y} = \frac{\partial φ}{\partial y} $$ $$x^{2}z + y^{2}z^{2} + h(z) = φ$$ => $$x^{2} + 2zy^{2} + \frac{\partial h}{\partial z} = \frac{\partial φ}{\partial z}=x^{2} + 2zy^{2}-1$$ $$-z+c = h$$, $$φ=x^{2}z + y^{2}z^{2} -z$$ QED
Problem 11.3 $$\textbf{F}$$ is a vector field $$xy^{2}i+2j+xk,$$ and L is a path parameterised by x = ct, y = c/t, z = d for the range 1 ≤ t ≤ 2. Evaluate $$ (a) \int_{L}{\textbf{F} dt} \hskip 1em (b)\int_{L}{\textbf{F} dy} \hskip 1em (c)\int_{L}{\textbf{F} \cdot d\textbf{r}}$$
My Answer:
(a)
$$\int_{L}{\textbf{F} dt} = \int_{L}{xy^{2} dt}i + \int_{L}{2 dt}j + \int_{L}{x dt}k$$
$$=(\int_{1}^{2}{xy^{2} dt})i + (\int_{1}^{2}{2 dt})j + (\int_{1}^{2}{x dt})k$$
$$=(\int_{1}^{2}{(ct)(\frac{c}{t})^{2} dt})i + 2j + (c[\frac{t^{2}}{2}]\bigg|_{1}^{2})k$$
$$=c^{3}(ln 2)i + 2j + \frac{3c}{2}k$$
(b)
$$\int_{L}{\textbf{F} dy} = \int_{L}{xy^{2} dy}i + \int_{L}{2 dy}j + \int_{L}{x dy}k$$
$$=(\int_{1}^{2}{(ct)(\frac{c}{t})^{2}(-\frac{c}{t^{2}}) dt})i + 2(\int_{1}^{2}{ (-\frac{c}{t^{2}} dt})j + (\int_{1}^{2}{(ct)(-\frac{c}{t^{2}}) dt})k$$
$$=(\int_{1}^{2}{(c^{4} (-\frac{1}{t^{3}}) dt})i + 2c(\int_{1}^{2}{ (-\frac{1}{t^{2}} dt})j + (\int_{1}^{2}{(ct)(-\frac{c}{t^{2}}) dt})k$$
$$=c^{4}(\frac{1}{4t^{4}})\rvert_{1}^{2}i + 2c (\frac{1}{t})\rvert_{1}^{2}j - c^{2} ln2k $$
$$=-\frac{3}{8}c^{4}i -cj - c^{2}ln2k$$
(c)
$$\int_{L}{\textbf{F} \cdot d\textbf{r}} = \int_{L}{xy^{2} dx} + {2 dy} + \int_{L}{x dz}$$
$$ = \int_{L}{xy^{2} (cdt)} + {2 (-\frac{c}{t^{2}}dt)} + 0$$
$$ = \int_{1}^{2}{(ct)(\frac{c}{t^{2}})c - 2(\frac{c}{t^{2}})dt}$$
$$ = \int_{1}^{2}{(\frac{c^{4}}{t}) - 2(\frac{c}{t^{2}})dt}$$
$$ = c^{4}ln2 + c \frac{2}{t}\rvert^{2}_{1}$$
$$=c^{4}ln2 - c$$ QED
Problem 11.5 Determine the point of intersection P, in the first quadrant, of the two ellipses $$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} = 1$$and $$\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}} = 1$$ Taking b < a, consider the contour L that bounds the area in the first quadrant that is common to the two ellipses. Show that the parts of L that lie along the coordinate axes contribute nothing to the line integral around L of xdy − ydx. Using a parameterisation of each ellipse of the general form x = X cosφ and y = Y sinφ, evaluate the two remaining line integrals and hence find the total area common to the two ellipses. Note: The line integral of xdy − ydx around a general closed convex contour is equal to twice the area enclosed by that contour.
My Answer: From the equations of ellipses provided by the questions, the point P must have x = y.Hence, $$x^{2}(\frac{1}{a^{2}}+\frac{1}{b^{2}}) => x = \frac{ab}{(a^{2}+b^{2})^{1/2}}$$ Denoting as curve $$C_1$$ the part of $$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} = 1$$ that lies on the boundary of the common region, we parameterise it by $$x = a cos \theta_1 \hskip 1em and \hskip 1em y = b sin \theta_1 \hskip 1em with \hskip 1em tan^{−1}(a/b) \leq \theta_1 \leq \pi/2.$$ Curve $$C_1$$ starts from P and finishes on the y-axis.
At P, $$a cos \theta_1= x = \frac{ab}{(a^{2}+b^{2})^{1/2}} => tan \theta_1 = \frac{a}{b}$$ Similarly, referring to that part of $$\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}} = 1$$ that lies on the boundary of the common region as curve $$C_2,$$ we parameterise it by $$x = b cos \theta_2 \hskip 1em and \hskip 1em y = a sin \theta_2 $$ with $$ 0 ≤ \theta_2 ≤ tan^{−1}(b/a).$$ On the x-axis, both y and dy are zero and the integrand xdy − y dx, vanishes.Similar for y-axis. $$I = \oint_L (xdy -ydx) $$ $$= \int_{C_2} (xdy -ydx) + \int_{C_1} (xdy -ydx)$$ $$= \int_{0}^{tan^{−1}(b/a)}{[ ab(cos \theta_2 cos \theta_2) \ - ab sin \theta_2(−sin \theta_2) ] d\theta_2} + \int_{tan^{−1}(a/b)}^{\frac{\pi}{2}}{[ ab(cos \theta_1 cos \theta_1) \ - ab sin \theta_1(−sin \theta_1) ] d\theta_1}$$ $$= ab(tan^{−1}(b/a)) + ab(\frac{\pi}{2} - tan^{−1}(a/b))$$ $$=2ab(tan^{−1}(b/a))$$ By the Green’s theroem, the area of a region R enclosed by a simple closed curve C is given by A = $$\frac{1}{2}(\oint_C (xdy -ydx))$$ The total common area in all four quadrants is $$4 \times \frac{1}{2} \times 2ab(tan^{−1}(b/a))=4ab(tan^{−1}(b/a))$$ Note that if we let b → a then the two ellipses become identical circles and we recover the expected value of $$\pi a^{2}$$ for their common area. QED