1.4 Normalization
Problem 1.4
(a) Let $$\int_{a}^{b}{| Ψ (x, t)|^{2}} dx = 1$$ $$\int_{0}^{a}{| A |^{2}} \frac{x^{2}}{a^{2}} dx + \int_{a}^{b}{| A |^{2}} \frac{(b-x)^{2}}{(b-a)^{2}} dx = 1$$ $$=\frac{A^{2}}{a^{2}} \frac{a^{3}}{3} + \frac{A^{2}}{(b-a)^{2}} \int_{a}^{b}(b-x)^2dx $$ $$=\frac{A^{2}}{a^{2}} \frac{a^{3}}{3} + \frac{A^{2}}{(b-a)^{2}}[-\frac{(b-x)^{3}}{3}] \rvert_{a}^{b}$$ $$=\frac{A^{2}a}{3} + \frac{A^{2}(b-a)}{3}$$ => $$A = \sqrt{\frac{3}{b}}$$
(b)
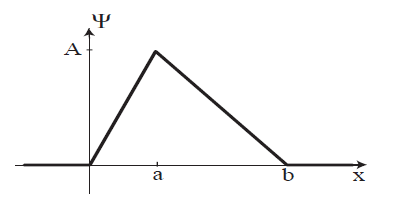
(c) At x=a
(d) $$P = \int_{0}^{a} A^{2} \frac{x^{2}}{a^{2}} dx=\frac{A^{2}}{a^{2}}(\frac{x^{3}}{3})\rvert_{0}^{a}=\frac{A^{2}a}{3}=(\sqrt(\frac{3}{b}))^{2}\frac{a}{3} = \frac{a}{b}$$
When $$b=a, P=1$$ When $$b=2a, P=\frac{1}{2}$$
(e) $$<x> = \int_{a}^{b}{x| Ψ (x, t)|^{2}} dx=\int_{0}^{a}{x \frac{A^2x^2}{a^2}} dx + \int_{a}^{b}{x\frac{A^2(b-x)^2}{(b-a)^2}} dx$$ $$=\frac{A^{2}}{a^{2}}\frac{x^{4}}{4}\rvert_{0}^{a} + \frac{A^{2}}{(b-a)^{2}}\int_{a}^{b}x(b-x)^{2}dx = \frac{3a^2}{4b} + \frac{3}{b(b-a)^2} \int_{a}^{b} (xb^{2} - 2bx^{2} + x^{3})dx$$ $$= \frac{3a^2}{4b} + \frac{3}{b(b-a)^2} (\frac{b^{2}x^{2}}{2}-\frac{2bx^{3}}{3} + \frac{x^{4}}{4})\rvert_{a}^{b} =\frac{b+2a}{4}$$ Q.E.D
Problem 1.5
(a)
Let $$\int^{\infty}_{-\infty}{|Ψ|^{2} }dx = 1$$
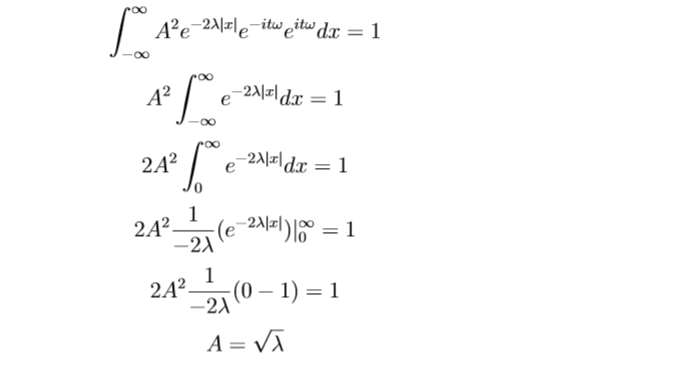
(b) $$<x> = \int_{-\infty}^{\infty}x\lambda e^{-2\lambda|x|} dx = 0, \text{as its odd function}$$ $$<x^{2}> = \int_{-\infty}^{\infty}x^{2}\lambda e^{-2\lambda|x|} dx$$ $$= 2\lambda \int_{0}^{\infty}x^{2}e^{-2\lambda|x|} dx$$ By the formula of exponential integral, $$=2\lambda ( 2! (\frac{1}{2\lambda})^{3})=\frac{1}{2\lambda^{2}}$$
(c)
$$\sigma^{2} = <X^{2}> - <X>^{2} = \frac{1}{2\lambda^{2}} - 0 = \frac{1}{2\lambda^{2}}$$
$$\sigma = \frac{1}{\lambda \sqrt{2}}$$
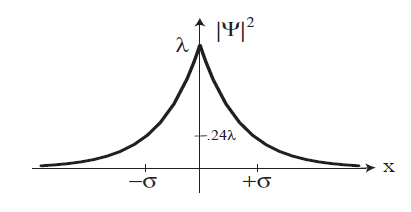Q.E.D
1.5 Momentumn
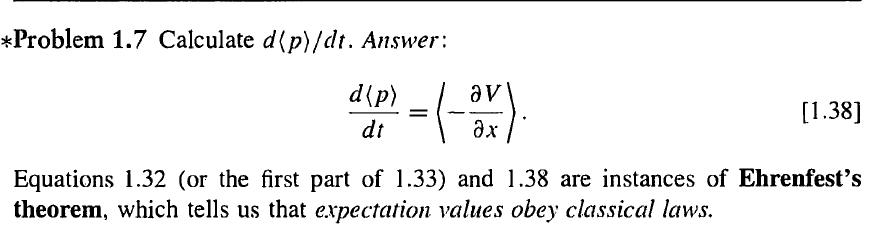Problem 1.7
$$<p> = m \frac{d<x>}{dt}$$
$$\frac{d<p>}{dt} = \frac{d^{2}<x>}{dt^{2}} = -i\hbar\int{\frac{\partial}{\partial t}(Ψ \frac{\partial Ψ}{\partial x})}dx$$
$$= -i\hbar\int{\frac{\partial Ψ*}{\partial t} \frac{\partial Ψ}{\partial x} + Ψ*\frac{\partial^{2} Ψ}{\partial t \partial x}} dx$$
By Schrodinger equation,
$$\frac{\partial Ψ*}{\partial t} = -i \frac{\hbar}{2m} \frac{\partial^{2} Ψ*}{\partial x^{2}} + \frac{i}{\hbar}VΨ*$$
$$= -i\hbar\int{(-i \frac{\hbar}{2m}\frac{\partial^{2} Ψ*}{\partial x^{2}} + \frac{i}{\hbar}VΨ*) \frac{\partial Ψ}{\partial x} + Ψ*\frac{\partial}{\partial x}( i \frac{\hbar}{2m}\frac{\partial^{2} Ψ}{\partial x^{2}} - \frac{i}{\hbar}VΨ)} dx$$
$$= -i\hbar\int{(-i \frac{\hbar}{2m}\frac{\partial^{2} Ψ*}{\partial x^{2}}\frac{\partial Ψ}{\partial x} + i \frac{\hbar}{2m}\frac{\partial^{3} Ψ}{\partial x^{3}}) + (\frac{i}{\hbar}VΨ* \frac{\partial Ψ}{\partial x} - \frac{i}{\hbar}Ψ*\frac{\partial }{\partial x} (VΨ))} dx$$
As $$-i\hbar(\int{-i \frac{\hbar}{2m}\frac{\partial^{2} Ψ*}{\partial x^{2}}\frac{\partial Ψ}{\partial x}} dx + \frac{i\hbar}{2m}(Ψ*\frac{\partial^{2} Ψ}{\partial x^{2}} - \int{\frac{\partial^{2} Ψ}{\partial x^{2}} \frac{\partial Ψ*}{\partial x}}dx))$$
$$=-i\hbar(\int{-i \frac{\hbar}{2m}\frac{\partial^{2} Ψ*}{\partial x^{2}}\frac{\partial Ψ}{\partial x}} dx + 0 - \frac{i\hbar}{2m}(\frac{\partial Ψ}{\partial x}\frac{\partial Ψ*}{\partial x}\rvert_{-\infty}^{\infty} - \int{\frac{\partial^{2} Ψ*}{\partial x^{2}}\frac{\partial Ψ}{\partial x}} dx ))$$
$$=-i\hbar(0+0)=0$$
$$\frac{d<p>}{dt} = -i\hbar \int{\frac{i}{\hbar}VΨ* \frac{\partial Ψ}{\partial x} - \frac{i}{\hbar}VΨ* Ψ\frac{\partial V}{\partial x} - \frac{i}{\hbar}VΨ* \frac{\partial Ψ}{\partial x}}dx$$
$$=-i\hbar\int{(-\frac{i}{\hbar}|Ψ|^{2}\frac{\partial V}{\partial x})}dx$$
$$=< -\frac{\partial V}{\partial x} >$$
Q.E.D
1.6 The Uncertainty Principle
Problem 1.9
(a)
$$Let \int_{-\infty}^{+\infty} |Ψ(x, t)|^{2}dx = 1$$
$$\int_{-\infty}^{+\infty} A^{2}(e^{-a(\frac{mx^{2}}{h}+it)} e^{-a(\frac{mx^{2}}{h}-it)})dx = 1$$
$$\int_{-\infty}^{+\infty} A^{2}e^{-2a(\frac{mx^{2}}{h})}dx = 1$$
By the formula of Guassian Integral,
$$A^{2} \sqrt{\frac{h\pi}{2am}} = 1$$
$$A=(\frac{2am}{h\pi})^{\frac{1}{4}}$$
(b)
$$\frac{\partial Ψ}{\partial t} = \frac{\partial }{\partial t}(A e^{-a(\frac{mx^{2}}{\hbar}+it)}) $$
$$= Ae^{-a(\frac{mx^{2}}{\hbar}}\frac{\partial }{\partial t}(e^{-iat})$$
$$= Ae^{-a(\frac{mx^{2}}{\hbar}}(e^{-iat})(-ia) = -iaΨ$$
$$\frac{\partial Ψ}{\partial x} = \frac{\partial }{\partial x}(A e^{-a(\frac{mx^{2}}{\hbar}+it)})$$ $$= A\frac{\partial }{\partial x}(e^{-a(\frac{mx^{2}}{\hbar})})(e^{-iat})$$ $$= Ae^{-iat}e^{-a(\frac{mx^{2}}{\hbar})}(-\frac{2xma}{\hbar})$$ $$=-\frac{2xma}{\hbar}Ψ $$
$$\frac{\partial^{2} Ψ}{\partial x^{2}} = -\frac{2ma}{\hbar}(Ψ + x\frac{\partial Ψ}{\partial x}) $$ $$= -\frac{2ma}{\hbar}(Ψ -\frac{2max^{2}}{\hbar}Ψ)$$ $$= -\frac{2ma}{\hbar}(1 -\frac{2max^{2}}{\hbar})Ψ$$ By the Schrodinger Equation, $$i\hbar(-aiΨ) = -\frac{\hbar^{2}}{2m}(-\frac{2ma}{\hbar}(1-\frac{2max^{2}}{\hbar})Ψ) + VΨ$$ $$a\hbar = a\hbar - 2ma^{2}x^{2} + V$$ $$V=2ma^{2}x^{2}$$
Further Problems For Chapter 1
$
